On Money-Pump Arguments

I recently ~read¹ Johan E. Gustafsson's Money-Pump Arguments (henceforth, MPA) and came away with a provisional conclusion that I don't buy into money-pump arguments.

Motivation

I started reading MPA because I was curious about the apparent solid arguments underpinning the vNM axioms. "Either you satisfy these axioms or you can be money-pumped." If true, this would pose challenge to claims of inadequacy of the vNM axioms and EUT as desiderata of rationality.

In particular:

• There have been some partial shutdown problem proposals relying on agent designs that don't satisfy the vNM completeness axiom.
  • In MPA, complete preferences are a prerequisite for constructing money pumps for transitivity, independence, and completeness.²
• Relatedly, Elliot Thornley & co argued that the MPA case for complete preferences is not as sound as it seems.
• Scott Garrabrant's counterexample of a rational non-independent preference and how it avoids being money-pumped.
  • From a personal conversation at ILIAD: ~"I think a utility function is actually a pretty innocent concept as long as you don't assume that it's linear with probabilities.".
• More broadly, interest in alternatives to expected utility and a suspicion that we've been over-indexing on economics-derived concepts.

My qualms about MPA

In the following, I'm going to use the word "pumper" to refer to the agent/thing that is exposing another agent to a money pump and extracting an arbitrary sum of money. I will call that latter pumped/exploited agent the "pumpee".³

1. Updatelessness invalidates Decision-Tree Separability

The entire chain of arguments given in MPA relies on the assumption of Decision-Tree Separability (henceforth, DTS).

The name comes from the fact that DTS is equivalent to "The decision-sub-tree rooted at any decision node can be separated/extracted/decontextualized from its decision-super-tree and the rational choice made at the node is the same in the contextualized and decontextualized situation.".

This assumption is wrong.

The core insight of updatelessness, subjunctive dependence, etc. is that succeeding in some decision problems⁴ relies on rejecting DTS. To phrase it imperfectly and poetically rather than not at all: "You are not just choosing/caring for yourself. You are also choosing/caring for your alt-twins in other world branches." or "Your 'Self' is greater than your current timeline." or "Your concerns transcend the causal consequences of your actions." or "Reification is not to be questioned and what has actually happened is not set in stone.".⁵

Gustafsson's arguments against foresight (section 2.1) and resoluteness (chapter 7) also rely on decision-tree separability. This brings us to my next qualm.

2. How strong does the pumper need to be?

A naive objection to MPA is:

As I just said, Gustafsson's objection to using foresight routes through DTS which I strongly disagree with.

But there's more. For a putative exploitation scheme to be an actual exploitation scheme, its option ontology needs to align with the exploitee's value ontology. Suppose you are in city A and somebody offers you to move you to city B for $1. You accept the trade. Then they offer you to move you back to city A for$1. You accept the trade again. They repeat the cycle 10 times, 100 times, 1000 times. "You are running in cycles, your intransitive (strict) preferences are non-transitive/cyclical and this makes you prone to the simplest forcing money pump." But perhaps the type signature of your object of wanting is not "location in city" but rather "trajectory between cities".

This in itself would not, perhaps, pose that much of a problem. Fine, let the arbitrarily intelligent/powerful pumper look into your brain, read out the type signature of your object of wanting and use it to construct the money pump. This presumes that the final outcome / object-of-wanting lens is the right model of values.⁶ A subtler — but related — issue is that the pumpee interprets the offers given by the pumper the way the pumper wants them to be interpreted and that the pumpee definitely is left worse off. However, interpretation is kind of up to the pumpee who may interpret the sequence of trades as overall worthy (see e.g. an example here). If the pumper gets to control the pumpee's interpretation, then the conclusion follows kinda trivially. Of course an agent that controls a load-bearing part of your cognition can exploit you.

Other tentative qualms

Here are some qualms that I'm less confident in their validity but I'm confident in them as trailheads.

How do you even encode the status quo?

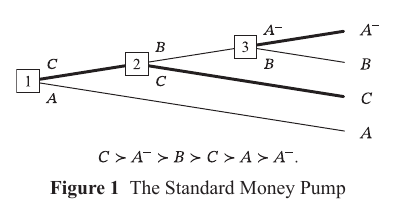
Money pumps like this one (from MPA) are to be interpreted as: "You start at node 1 with A. You are offered to exchange it for C (go up) or keep it (go down).". However, you can flip the tree and get something formally equivalent but with a very different interpretation. I don't know if it matters but feels sus.

!Pasted image 20241023110846.png

Final outcomes and (in)finite games

Is it necessarily true that everything the agent cares about is describable and is it necessarily true that it's about something final? I don't know and I'm suspicious. I'm more suspicious towards finality. Compare: If you believe your iterated Prisoner's Dilemma (PD) plays out for any finite number of turns, it is equivalent to a single-turns PD, and you defect. If you believe it plays out for infinitely many turns, then you are incentivized to cooperate. By applying a more enlightened decision theory, you transcend to logical time and all games become (infinitely) iterated games. Again, this is just a trailhead.

Universal totally ordered resource

Another qualm of mine was that money pumps rely on some totally ordered resource that the agent values (something like "a continuous chain in their preference preorder"), i.e. eponymous "money". Gustafsson mostly does without "money" in his "money pumps" by introducing the unidimensional continuity of preference which basically amount to "Any state that you value can be improved/worsened by an arbitrary amount.".

A sketch of the boundary/intersection between the MPA view and my "positive" view

I think transitivity is correct, even though what seems like a violation of transitivity may actually be something more complicated. I don't want stuff to hinge on preference incompleteness. I do see the arguments for continuity/independence but I also not-see the arguments for them, probably indicating some form of Gestalt switching that is relevant here. I don't think final outcomes are the right ontology.